
This demonstration is based on the research titled “A DCT-domain System for Robust Image Watermarking” by Mauro Barni, Franco Bartolini, Vito Cappellini, and Alessandro Piva.
Presented by: Ordaneza, Jethro D., BSCS
What is Discrete Cosine Function?
The Discrete Cosine Transform (DCT) is a highly favored transformation function employed in signal processing. It serves to convert a signal from the spatial domain into the frequency domain. Owing to its outstanding performance, it has found extensive utilization in the JPEG standard for image compression. The DCT has been effectively employed across various domains, including data compression, pattern recognition, image processing, and more.
Methodology
The paper presents a watermarking algorithm for digital images operating in the frequency domain. It embeds a pseudo-random sequence of real numbers, following a normal distribution with zero mean and unity variance, into a selected set of DCT coefficients.
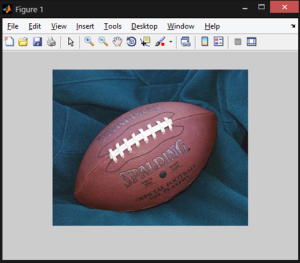
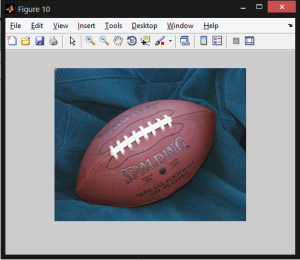
The code for acquiring the image is demonstrated below:
% acquiring the first image
img = double(imread('football.jpg'));
figure, imshow(img/255); % shows the original image
img2 = img;
[row, column, depth] = size(img);
Output image:
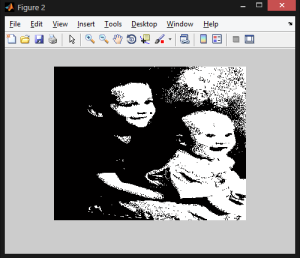
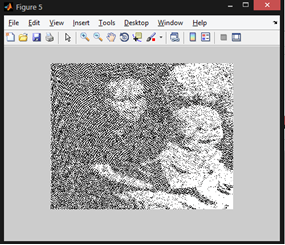
The following code demonstrates the process of acquiring the image to be used as a watermark:
% acquiring the watermark image
[watermark map] = imread('kids.tif');
watermark = imresize(watermark,[row column]);
watermark = im2bw(watermark,map, 0.5);
figure, imshow(watermark);
Output image:
Watermarking
To apply the watermark to the image, we initially need to extract the RGB components of the original image. The following code illustrates this process:
% Watermarking
r = img(:,:,1);
g = img(:,:,2);
b = img(:,:,3);
The subsequent step involves applying the Discrete Cosine Transform (DCT) to the RGB components of the original image. We will utilize the MATLAB function dct2() to apply the discrete cosine transform function.
dr = dct2(r);
dg = dct2(g);
db = dct2(b);
A coefficient, denoted as “cof,” will be employed to represent the strength of the watermark:
cof = 10; % Coefficient of watermark's strength
In this context, a value of 10 is utilized to indicate the watermark’s strength.
The next step involves embedding the watermark into the RGB components of the original image after applying the DCT.
[rowM,colM] = size(watermark);
dr(1:rowM,1:colM) = dr(1:rowM,1:colM) + cof * watermark;
dg(1:rowM,1:colM) = dg(1:rowM,1:colM ) + cof * watermark;
db(1:rowM,1:colM) = db(1:rowM,1:colM) + cof * watermark;
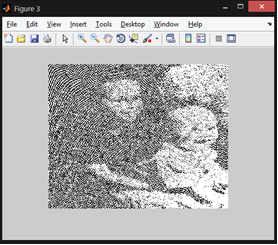
figure,imshow(dr);
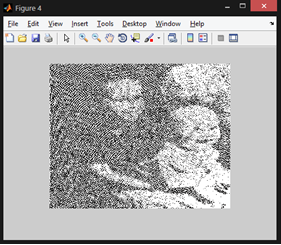
figure,imshow(dg);
figure,imshow(db);
Red component
Green component
Blue component
The zigzag scanning permutation is employed to distribute energy from high to low, mirroring the transition from low frequency to high frequency. Human eyes are more sensitive to noise in the lower-frequency band than in the higher frequency.
Natural images predominantly exhibit energy concentration in the lower frequency range. Consequently, a watermark concealed in the higher frequency band could potentially be lost after undergoing lossy compression.
The subsequent step involves obtaining the inverse discrete cosine function of the RGB components with the embedded watermark. The resulting RGB component from the inverse discrete cosine function will be utilized to generate the final watermarked image.
% inverse discrete cosine function
r2 = idct2(dr);
g2 = idct2(dg);
b2 = idct2(db);
img2(:,:,1) = r2;
img2(:,:,2) = g2;
img2(:,:,3) = b2;
figure,imshow(r2);
figure,imshow(g2);
figure,imshow(b2);
figure,imshow(img2);
figure ; imshow(img2/255)
figure ; imshow(abs(img2-img)*100) %comparison
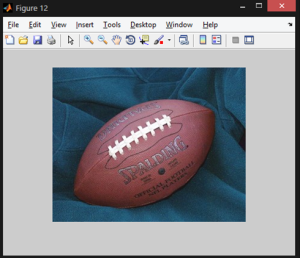
Below, you can view the final watermarked image:
Dewatermarking
Watermarking and dewatermarking processes share similar steps. In watermarking, we embed the watermark by adding the product of the coefficient and the watermark image to the DCT of the original image. In dewatermarking, we use the same watermark image and the coefficient initially used to embed the watermark into the original image.
Here, we subtract the product of the coefficient and the watermark image from the DCT of the watermarked image. The code for this process is provided below:
% De-watermarkig
% Clean image (known mask)
img2 = img3 ;
dr2 = dct2(img2(:,:,1));
dg2 = dct2(img2(:,:,2));
db2 = dct2(img2(:,:,3));
dr2(1:rowM,1:colM) = dr2(1:rowM,1:colM) - cof * watermark;
dg2(1:rowM,1:colM) = dg2(1:rowM,1:colM) - cof * watermark;
db2(1:rowM,1:colM) = db2(1:rowM,1:colM) - cof * watermark;
deImage(:,:,1) = idct2(dr2);
deImage(:,:,2) = idct2(dg2);
deImage(:,:,3) = idct2(db2);
figure ; imshow(deImage/255)
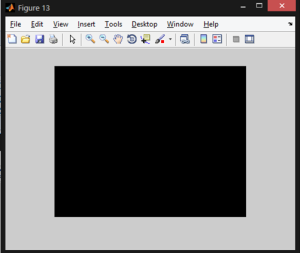
figure ; imshow(abs(deImage-img)*10000) %comparison showing all black image for no difference
Below, you can see the retrieved image:
A comparison between the retrieved image and the original image is presented below. If there is no difference between the two images, the comparison will display an all-black image.
You can download the research from this link, and the full code and PowerPoint presentation are available here.
Thank you for reading!
References
[1] Arai, Y.; Agui, T.; Nakajima, M. (November 1988). ”A fast DCT-SQ scheme for images”.
[2] Barni, M.; Bartolini, F.; Cappellini, F.; Piva, A. (February 1997). ”A DCT-domain system for robust image watermarking”.