Fixed Linear Correlation Embedder and Linear Correlation Detection

This demo is based on the book “Digital Watermarking and Stenography” by Cox et al.

Presented by:
Jethro D. Ordaneza, BSCS
Iana Kristine D. Yu, BSCS

This system employs a blind embedding algorithm, distinct from E_BLIND/D_LC. To grasp the new algorithm, let’s first explore E_BLIND/D_LC’s approach.

Blind Embedding and Linear Correlation Detection

This system’s detection algorithm utilizes linear correlation as its metric. It encodes a single bit of information, making m either 1 or 0 for simplicity.

E_BLIND Embedder

This system employs a single reference pattern, Wr, with pixel intensities matching the cover image’s size. The message pattern, Wm (encoding a 1-bit message m), is set as either Wr or -Wr, based on m (1 or 0). An input parameter, a, scales Wm, governing the visibility and watermark robustness tradeoff. Consequently, the blind embedding algorithm calculates the following:

Wm = Wr, if m = 1
Wm = -Wr if m = 0
Wa = aWm
Cw = Co + Wa

E_FIXED_LC Embedder

In this embedder, watermarking utilizes a novel algorithm to guarantee 100% embedding effectiveness. This is achieved by adjusting the embedding strength a to ensure all watermarked images maintain a fixed-magnitude linear correlation with the reference pattern.

To ascertain the required embedding strength, we initially calculate the inherent correlation between the cover work and the message pattern, Co * Wm / N. Our objective is to maintain a constant magnitude of detection strength that consistently exceeds the detection threshold, expressed as Tlc + B. Here, Tlc represents the detection threshold, and B > 0 serves as an embedding strength parameter. The magnitude of the detection value obtained from an image immediately after embedding is defined as:

Zlc(Cw,Wm) = 1/N(Co*Wm + Wa * Wm)

Here, Wm stands for the message pattern, and Wa = aWm/. By substituting Tlc + B for Zlc(Cw,Wm) and solving for a we derive:

a = (N(Tlc + B) – Co * Wm)/(Wm * Wm)

D_LC Detector

To detect the watermark, we must identify the signal Wr. The optimal method for detecting this signal involves calculating the linear correlation between the received image, C, and the reference pattern, Wr, as follows:

Zlc(C,Wr) = 1/n * (C * Wr) = 1/N * sum(c[x,y] * Wr[x,y])

sum() – summation

Here, c[x,y] and Wr[x,y] represent the pixel values at location x,y in C and Wr, respectively, with N denoting the total number of pixels in the image. To determine the presence of a watermark, we apply a threshold Tlc to the magnitude of Zlc. If |Zlc(C,Wr)| < Tlc, the detector indicates the absence of a watermark. Consequently, the D_LC detector produces the following output:

M = 1, if Zlc(C,Wr) > Tlc
M = no watermark, if -Tlc <= Zlc (C,Wr) <= Tlc
M = 0, if Zlc(C,Wr) < -Tlc

The detection threshold directly impacts the false positive rate. A lower threshold increases the likelihood of classifying an unwatermarked work as watermarked.

Coding

This code is for the E_FIXED_LC/D_LC watermarking system, derived from Chun-Wei Cheng’s demo.

The first step is to read the image that will serve as the cover work.

% Read image 
cover = double(imread('cameraman.tif'));
original = im2double(imread('cameraman.tif'));

figure, imshow(original);

[Cx,Cy]=size(cover);

The following code demonstrates how to generate the watermark pattern intended for embedding into the cover work.

%Generate Reference Pattern 
random = rand(Cx,Cy);
randomMean = mean2(random);
randomDifference =(random - randomMean);

pattern = randomDifference/std2(randomDifference);

figure;imshow(pattern,[]);

Next, we’ll determine the embedding strength ‘a’ or ‘alpha’ to be utilized by the embedder.

alpha1 = ( x * y * beta - sum(sum(cover(:).*pattern(:)))) / (sum(sum(pattern(:).*pattern(:))));
alpha2 = ( x * y * beta - sum(sum(cover(:).*-pattern(:)))) / (sum(sum(-pattern(:).*-pattern(:))));

We use alpha1 for bit-1 and alpha2 for bit-0. Subsequently, we proceed to embed the watermark into the cover work.

%Bit 1 
cw1 = cover + wa1;
cw1 = double(uint8(cw1));

%Bit 0 
cw2 = cover – wa2;
cw2 = double(uint8(cw2));

%Bit 
cw3 = double(uint8(cover));

For detection, we calculate the linear correlation between the resulting image and the watermark pattern used, as demonstrated by the following code.

cor = sum(sum(cw(:).*pattern(:))) / ( x * y );

The cor variable represents linear correlation, cw corresponds to the cover work, and pattern denotes the watermark pattern.

We’ve developed a system with a graphical user interface (GUI). You can obtain the complete code by downloading it here. The downloaded zip file will contain two .m files: System2.m, which is the program without GUI, and final.m, which contains the program with GUI. The system with the GUI is displayed in the images below.

Here’s an example of the initial user interface of the system:

Upon uploading a cover work, the system will generate three images: one with a bit-1 message watermarked (cw1), another with a bit-0 message watermarked (cw2), and a third without any watermark (cw3). Additionally, it will export the watermark pattern.

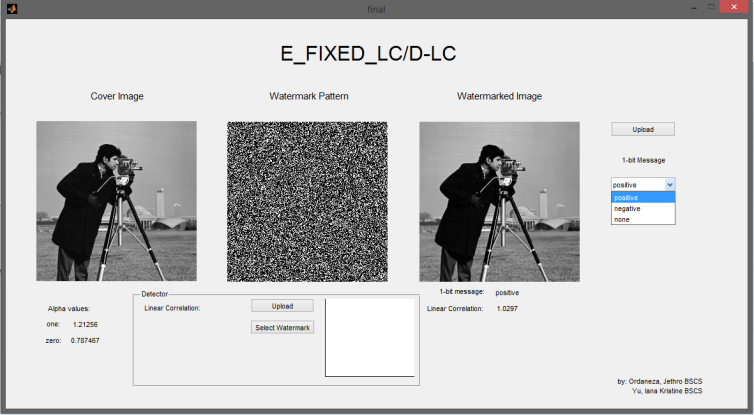
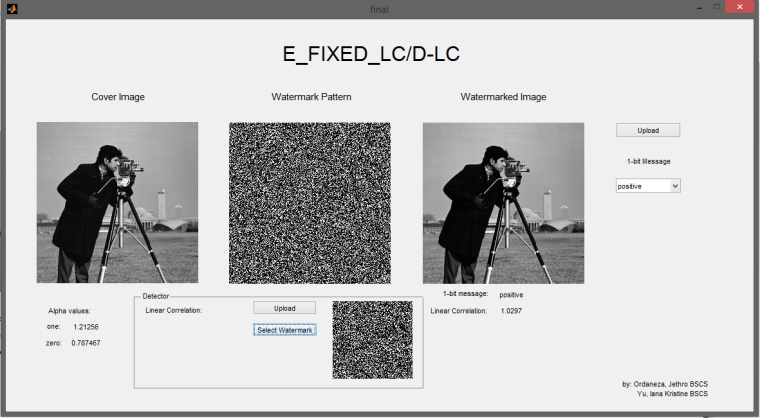
In the watermark detector, start by selecting the watermark pattern, and then upload the image you wish to test to determine if the selected watermark pattern has been embedded in it.

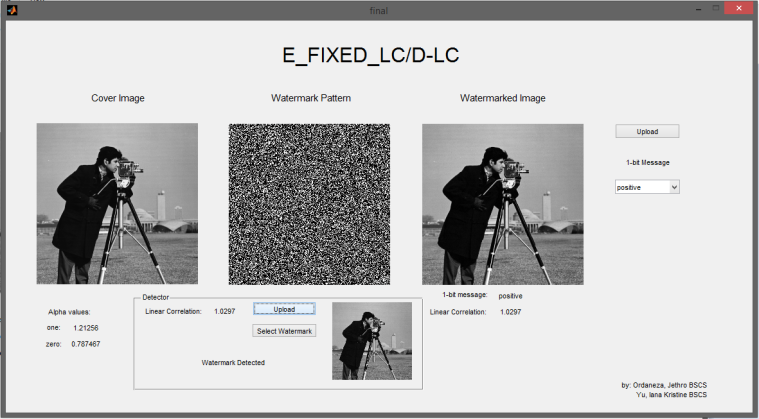
Once you’ve uploaded the image, the system will proceed to detect whether the image has been watermarked or not.

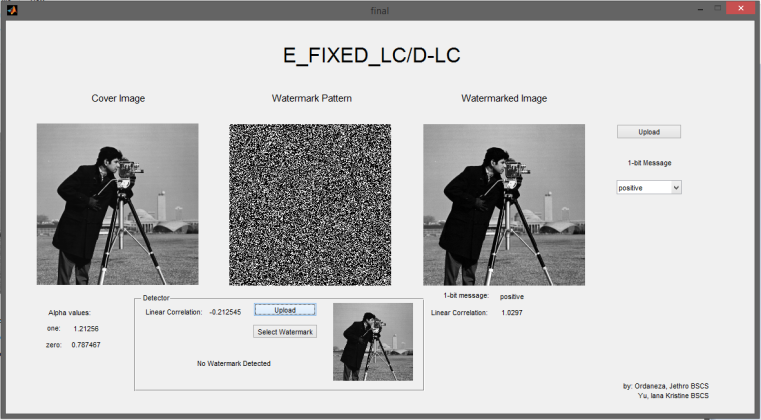
Thank you for reading!

References

[1] Cox, I.; Miller, M.; Bloom, J.; Fridrich, J.; Kalker, T. ”Digital Watermarking and Stenography”.